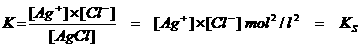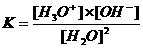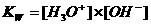EVENWICHTSREACTIES
Inleiding
Elke scheikundige reactie begint met reagentia (de reagerende stoffen) om producten te maken. Het lijkt zo eenvoudig, maar dat is het niet altijd. In de praktijk hebben de meeste producten op hun beurt weer de neiging om terug te reageren en zo de uitgangsstoffen terug te vormen. In zulke gevallen spreken we van een "heen-en-terug-reactie"
Voorbeeld:
Heenreactie:
I2+ H2  2HI
2HI
Terugreactie:
2HI  I2+ H2
of:
I2 + H2
I2+ H2
of:
I2 + H2  2HI
2HI
De gewoonte in de scheikunde is om die twee pijlen / die twee reacties, te combineren tot één reactie met een dubbele pijl:
I2+ H2  2HI (ΔH < 0)
2HI (ΔH < 0)
Nóg een gewoonte in de scheikunde is om het energie-effect erbij te zetten; naast de reactievergelijking, normaal behorende bij de heenreactie:
ΔH>0 of ΔH<0.
In het bovenstaande voorbeeld betekent ΔH<0 dat de heenreactie exotherm is
Hetzelfde evenwicht kunnen we ook op de volgende manier schrijven:
2HI  I2+ H 2 (ΔH > 0)
I2+ H 2 (ΔH > 0)
Deze module 8 behandelt dit type reacties.
zie ook: wikipedia
Inhoud van de module
1. Reversibiliteit en rendement
2. Zwak en sterk; spontaniteit
2.1 Een beetje Thermodynamica
3. De evenwichtsvoorwaarde
3.1 Het dynamisch evenwicht
4. De evenwichtskonstante
5. Le Chatellier & en van ‘t Hof
5.1 Bevriezing van het evenwicht
5.2 Het effect van de katalysator
6. Homogeen en heterogeen evenwicht
7. Extreme waarden van K
7.1 KC en KP
7.2 KS en Oplosbaarheidsproduct
7.3 Kw en autoprotolyse van water
Dit hoofdstuk behandelt de zogenaamde 'evenwichtsreacties', waarin producten worden gevormd en met dezelfde snelheid weer terug reageren.
Zulke reacties noem je: reversibel
Vergeet na dit hoofdstuk niet dat er ook irreversibele reacties zijn, dus reacties die echt maar één kant opgaan. De ontstane producten reageren dan niet meer terug.
Denk bijvoorbeeld aan een verbrandingsreactie: de producten water en kooldioxide reageren echt niet meer spontaan terug om weer benzine en zuurstof te worden.
Je kunt je afvragen wat het nut is van zo'n evenwichtsreactie, als de gevormde producten toch weer terugreageren. Wat is het rendement van zo'n reactie?
Wil je een redelijke opbrengst dan moet er aan een paar voorwaarden worden voldaan. Je kunt zo'n evenwicht beïnvloeden op verschillende manieren. Op die manier kun je toch een evenwicht zoveel mogelijk aan de kant van de producten houden.
Een reversibele reactie bestaat dus feitelijk uit twee reacties. Die twee reacties worden samengesteld tot één. In de reactievergelijking gaan de twee pijlen van de twee reacties twee kanten op.
Verder mag je in het algemeen verwachten dat aan één kant van de pijlen de sterkere stoffen staan en aan de andere kant zwakkere.
Zoals het woord al suggereert: de sterkere stoffen hebben een sterkere neiging tot reageren dan de zwakkere.
En stoffen die reageren zullen voor een groot deel verdwijnen, terwijl de zwakke juist gevormd worden.
Heel bijzonder dus, speciaal voor chemische evenwichten geldt:
De sterken re(a)geren ten gunste van de zwakken
|
En dat doen ze nog spontaan ook. Kom daar eens om in onze moderne samenleving!
De zwakke stoffen reageren ook wel (terug), maar met weinig kracht en weinig rendement.
Alleen met externe dwang kunnen zwakke stoffen gedwongen worden tot vollediger doorreageren.
Als dat gedaan wordt is er geen sprake meer van een spontane reactie.
In module 7 bespraken we al een stukje thermodynamica van reacties in het algemeen en ook het begrip "spontaan".
Stel je het volgende chemische systeem voor:
N2 + 3H2  2NH3 (ΔH < 0 en ΔS < 0)
2NH3 (ΔH < 0 en ΔS < 0)
Zo'n chemisch systeem betekent bijvoorbeeld dat stikstof, waterstof en ammoniak zich samen, al reagerend, bevinden in een cilinder onder een zuiger.
Denk vervolgens aan die formule:
ΔG = ΔH - TΔS
De heenreactie (de vorming van ammoniak) is exotherm (ΔH < 0) en dat garandeert een zekere spontaniteit van de reactie naar rechts.
Aan de andere kant echter: de terugreactie houdt toename van de entropie in
(het aantal deeltjes neemt toe, verdubbelt in het voorbeeld, en dus de mate van wanorde wordt groter bij reactie van rechts naar links en dat garandeert ook een zekere spontaniteit voor de terugreactie. (ΔS neemt dus toe bij de terugreactie en neemt af bij de heenreactie)
Dus in het voorbeeld hebben beide reacties, de heen- en de terug-, een zekere sponaniteit om verschillende redenen.
In de formule ΔG = ΔH - TΔS, toegepast voor de heenreactie, heeft zowel ΔH als ΔS een negatieve waarde.
Wiskundig gezien betekent dit dat ΔH de waarde van ΔG negatiever maakt, terwijl de term -TΔS de waarde van ΔG positiever zal maken.
Het kan voorkomen dat de twee termen (ΔH= TΔS) gelijk aan elkaar zijn zijn, afhankelijk van de omstandigheden.
We raken hier aan een thermodynamisch geheim:
- Op het moment dat de waarde van ΔG gelijk wordt aan 0, wordt het chemisch evenwicht bereikt.
- Als ΔG > 0 , dus als de vrije energie van het systeem toeneemt, domineert de terugreactie (verplaatsing van het evenwicht naar links).
- Als ΔG < 0 , dus als de vrije energie van het systeem afneemt, domineert de heenreactie (verplaatsing van het evenwicht naar rechts).
Je ziet: wil je het scheikundig evenwicht goed begrijpen dan moet je het begrip "entropie" kennen.
In module 7 wordt het volgende behandeld over de reactiesnelheid:
V = k.[conc.]n
- V : de snelheid;
- k : de samenstelling van andere konstante factoren;
- n : de coëfficiënt van het reagens in de reactievergelijking;
Als je deze formule toepast op zowel de heen- als de terugreactie
2HI  I2 + H2
I2 + H2
komen we bij het volgende resultaat:
Vheen = kheen x [HI]2
en
Vterug = kterug x [I2] x [H2]
Let op: in principe zullen de concentraties van de stoffen in een evenwicht nooit helemaal 0 worden, en dat wil zeggen dat ook de snelheden niet 0 worden, zoals dat wel gebeurt bij éénrichtingsreacties.
Opdracht 1
De reactiesnelheid is voor een groot deel afhankelijk van concentraties van de reagerende stoffen:
hoe meer substraat (reagerende stof), hoe sneller de reactie.
- Dus op welk moment van de reactie zal de reactiesnelheid het grootste zijn?
- En dezelfde vraag voor de terugreactie.
- Hieronder vind je diagrammen van de snelheden en van de concentraties:
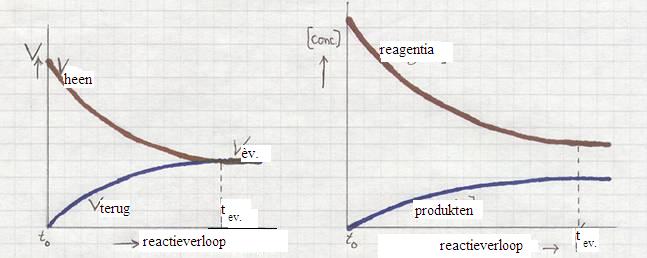
Hoe veranderen de reactiesnelheden van de heen- en terugreactie vanaf de start (t0) tot het bereiken van het evenwicht (teq)?
De evenwichtsvoorwaarde van een chemisch evenwicht is:
de twee reacties (heen en terug) worden niet 0 (behouden een zekere snelheid) en verlopen met gelijke snelheid.
of ook: Vheen = Vterug
Opdracht 2
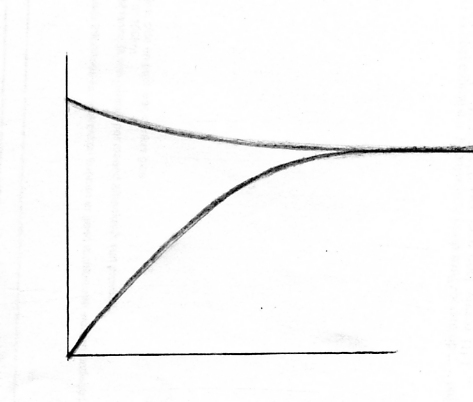
- Zet in het snelheidsdiagram de eenheden en geef aan wat de x-as en y-as voorstellen.
- Welke stoffen zullen gaan domineren gedurende het evenwicht en waarom?
Feitelijk is elke chemische evewichtsreactie een dynamisch evenwicht.
Van buitenaf bekeken lijkt het of er niets gebeurt, maar de werkelijkheid is dat er twee tegengestelde reacties plaats vinden, elk met dezelfde snelheid. Ze reageren dus voortdurend, de uitgangsstoffen zowel als de producten, maar je ziet er niets van.
Zo'n chemisch evenwicht wordt ook "het dynamische evenwicht" genoemd.
Opdracht 3
Een systeem in chemisch evenwicht:
- heeft gelijke hoeveelheden van reagentia en producten
- heeft geen verandering in de hoeveelheden producten en reagentia
- wordt door temperatuursverandering niet beïnvloed
- kan verschoven worden door een katalysator
Leg je keuze uit.
Vheen = kheen x [I2] x [H2]
en
Vterug = kterug x [HI]2
We weten dat bij evenwicht de heen- en de terugreactie even snel verlopen:
Vheen = Vterug
Oftewel:
kheen x [I2] x [H2] = kterug x [HI]2
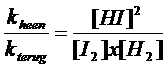
Let op: het quotiënt van de twee constantes geeft een nieuwe constante; we mogen dus schrijven:
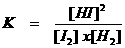
K noemen we: "de evenwichtsconstante"
Een diepgaander beschouwing over de K (evenwichtsconstante) is te vinden op wikipedia
Opdracht 4
Welke waarde zal K (min of meer) hebben in het geval dat de reagentia en de producten ongeveer gelijke reactiekracht hebben?
Leg je antwoord uit.
Opdracht 5
Maak een diagram van de concentraties van de reagentia en de producten tegen tijd.
glucose + fructose  saccharose + water ΔH < 0
saccharose + water ΔH < 0
Het betreft een homogene reactie in evenwicht die begon op moment t = 0 (in minuten) bij de constante temperatuur van 25ºC.
Concentratie
van
sacharose |
Concentratie
van
glucose |
Concentratie
van
fructose |
Duur
van de
reactie
in minuten |
|
1,00 |
1,00 |
0 |
0,20 |
0,79 |
|
60 |
|
|
0,67 |
120 |
0,40 |
0,60 |
|
180 |
|
|
|
240 |
0,50 |
|
|
300 |
Schets de grafiek die de verandering toont van de concentraties van saccharose en fructose tegen de tijd
Dit zijn de namen van twee wetenschappers die (1888) het chemisch evenwicht uitvoerig onderzochten en tot de volgende conclusie kwamen:
Als je van buitenaf een verandering aanbrengt aan een chemisch evenwicht
veroorzaakt dat een verschuiving van het evenwicht op zodanige manier
dat die uitwendige verandering tegengewerkt wordt,
zoveel mogelijk ongedaan wordt gemaakt.
Met andere woorden:
Als je een systeem in evenwicht verstoort,
zal dat systeem de neiging hebben om de effecten van die verstoring minimaal te maken.
Dat gaat net zolang door tot er een nieuw evenwicht is ingetreden.
Dit principe is vernoemd naar de Franse scheikundige Henry Louis Le Chatelier, die het in 1884 formuleerde. Het wordt ook wel het principe van Le Chatelier en Van 't Hoff genoemd, naar de Nederlandse scheikundige Jacobus van 't Hoff. Het principe is gebaseerd op het feit dat de evenwichtsconstante voor een gegeven reactie constant is bij een bepaalde temperatuur.
Zo'n externe verandering, zo'n beïnvloeding zou bijvoorbeeld kunnen zijn:
- één van de stoffen wordt extra toegevoegd,
- het volume verandert
- er wordt warmte toegevoegd,
- of iets dergelijks.
Hieronder gaan we hier wat in detail op in:
- We veranderen de hoeveelheid van een aan het evenwicht deelnemende stof
bijvoorbeeld: waterstof toevoegen veroorzaakt een verschuiving van het evenwicht dat er voor zorgt dat (een deel van) dit extra waterstof weer (gedeeltelijk) verdwijnt, door de heenreactie te stimuleren.
Dit gaat door totdat er een nieuw evenwicht is bereikt.
-

In de beker bevindt zich NH3(aq) (basisch milieu) met een paar druppels van de indicator methylrood,
waarvan de afgekorte formule is: HIn
Dan stelt zich in de oplossing het volgende evenwicht in:
HIn  H++ In-
H++ In-
Rood Geel
De aanwezigheid van een base (die H+ opneemt) betekent een verschuiving van het evenwicht naar rechts
 de gele kleur domineert.
de gele kleur domineert.
-

Je voegt nu een beetje HCl(aq) toe, waardoor het basisch milieu verandert naar zuur milieu.
Het zuur wil H+ afstaan, dus:
het evenwicht: HIn  H++ In-
H++ In-
Rood Geel
verplaatst zich naar links en de rode kleur gaat domineren.
-

Nu gaan we weer base toevoegen: (NH3(aq)), de kleur verandert weer naar geel
dus hetzelfde evenwicht verplaatste zich nu weer naar rechts:
HIn  H++In-
H++In-
Rood Geel
-

Dit gedoe kun je eindeloos herhalen.
Elke keer zal het evenwicht verschuiven naar rechts of naar links.
De totaal-situatie in de beker verandert eigenlijk maar heel weinig.
Het is alleen maar een geringe verschuiving van het evenwicht naar de ene of ander kant, afhankelijk van de omgeving, het milieu.
- Het Volume veranderen
Een groter volume betekent dat er meer ruimte komt voor de deelnemende deeltjes in het evenwicht.
Hoe kan het systeem deze verandering tegenwerken? Hoe kan het systeem die meer ruimte voor deeltjes compenseren?
Het principe is dat zo'n verandering wordt tegengewerkt door het evenwicht, en dat kan alleen als er meer deeltjes worden gevormd.
Je kunt het volume op verschillende manieren veranderen:
- bij gassen kan dat direct, door bijvoorbeeld een zuiger uit te trekken en de cylinder zo meer inhoud te geven
- bij vloeistoffen kun je verdunnen
In beide gevallen is het effect gelijk.
In het voorbeeld van HI is dat niet mogelijk, want aan elke kant staan evenveel deeltjes. Verschuiving naar links of naar rechts levert dus niets op.
In dit geval heeft verandering van volume geen invloed op de ligging van het evenwicht.
- Warmte toevoegen of onttrekken
Als je extra energie toevoegt aan een chemisch evenwicht zal ook weer geprobeerd worden die verandering tegen te werken. In dit geval kan die toegevoegde warmte (voor een deel) worden opgebruikt door de endotherme reactie.
In het geval van HI zal het evenwicht zich naar links verplaatsen
[glucose + fructose  saccharose + water ΔH < 0]
saccharose + water ΔH < 0]
Het saccharose-evenwicht is exotherm naar rechts.
Bij verlaagde temperatuur zal er dus minder energie beschikbaar zijn en wil het evenwicht energie "erbij maken".
Dat kan gerealiseerd worden met de exotherme reactie, dus met de reactie naar rechts. Oftewel, bij lagere temperaturen vormt zich meer saccharose.
Dit alles werd hierboven op een kwalitatieve manier bekeken.
Je kunt dezelfde effecten ook kwantitatief onderzoeken en bewijzen met behulp van de evenwichtsconstante.
Die heeft een vaste waarde en verandert niet, wat je ook aan het evenwicht doet (behalve temperatuursverandering).
Die bewijzen kun je leveren met wiskundige berekeningen.
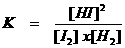
Stel bijvoorbeeld dat de hoeveelheid I2 verhoogd wordt.
Kijk naar de wiskundige formule voor K. Als de [I2] hoger wordt en K mag niet veranderen, dan moet, wiskundig gezien, ook de hoeveelheid HI hoger worden, dus moet het evenwicht zich verplaatsten.
Tollen's Reagens
Ag+-ionen zijn zwakke oxidatoren die bijvoorbeeld glucose kunnen oxideren (de aldehydegroep daarin).
De vergelijking van de oxidatie is als volgt:
2Ag++ C6H12O6 + H2O
 2Ag(s)+ C6H12O7 + 2H+ ΔH > 0 ( evenw. 1)
2Ag(s)+ C6H12O7 + 2H+ ΔH > 0 ( evenw. 1)
Om dit evenwicht naar rechts te dwingen heb je twee mogelijkheden: het basisch milieu versterken en verwarmen.
Basisch milieu:
Ag+-ionen, gebracht in basisch milieu, vormen een neerslag: AgOH, en daaruit ontstaat al heel gauw: Ag2O met een bruine kleur en in vaste vorm.
Echter, Ag+ reageert alleen redelijk goed als oxidator als het vrij is, in opgeloste vorm dus; niet als het vast zit aan OH- of aan O2-.
Wil je dus dit ion als oxidator toepassen, dan moet je het in vrije ionvorm hebben, zelfs in basisch milieu.
Er is een mogelijkheid om dat te realiseren, namelijk: ammoniak toevoegen (NH3(aq)), dat de Ag+-ionen op de volgende manier in oplossing houdt:
Ag+ + 2NH3  Ag(NH3)2+
Ag(NH3)2+
Op deze wijze blijven de Ag+-ionen in oplossing, zelfs in basisch milieu.
Een aardige beschrijving van een proef met Tollens Reagens vind je hier en ook hier.
Dat de proef met tollens reagens ook vaak 'de zilverspiegelproef' wordt genoemd, komt doordat bij deze reactie puur zilver (Ag(s)) gevormd wordt, dat zich afzet op de wand van een reageerbuis. Er ontstaat daarbij een echt spiegeloppervlak.
Opdracht 6a:
Leg uit hoe ammoniak het hierbovenstaande evenwicht beïnvloedt.
Verhoging van Temperatuur:
Een endotherme reactie kost energie, dus, extra energie ondersteunt de endotherme reactie.
Opdracht 6b:
Leg uit hoe temperatuursverhoging het evenwicht beïnvloedt.
Opdracht 7
Enkele evenwichten in het menselijk lichaam, in dit geval in het bloed, zijn:
HHb + O2  HbO2 + H+
HbO2 + H+
CO2 + H2O  H2CO3
H2CO3
H2CO3  H+ + HCO3-
H+ + HCO3-
Welke problemen kunnen mensen met een te lage bloed-pH hebben?
antwoord 08-07
Opdracht 8
Ammoniak is een gasvormige stof die goed in water oplost:
NH3(g)  NH3(aq)
NH3(aq)
Het lost niet alleen op in water, maar reageert er ook mee:
NH3 + H2O  NH4+ + OH-
NH4+ + OH-
Het hydroxide ion is een sterke base (veel sterker dan ammoniak), en daarom heeft de heen-reactie een terugreactie.
In de ammoniak-oplossing ligt dit evenwicht behoorlijk ver naar links.
- wat zal er gebeuren als er wordt toegevoegd:
- natriumhydroxide
- zoutzuur
- Leg uit of de waarde van K groot of klein zal zijn
- Welke zijn hier de sterke en de zwakke stoffen?
Opdracht 9
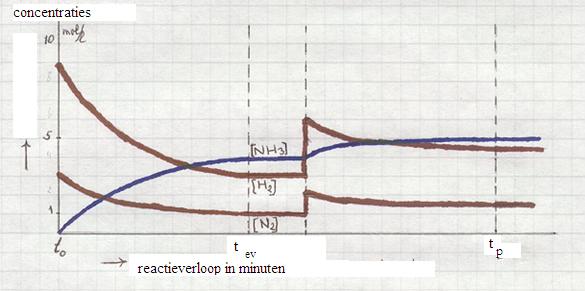
- Analyseer het diagram van de reactie van de gassen waterstof en stikstof, waarbij ammoniakgas wordt gevormd (synthese van Haber-Bosch).
- Wat zal er gebeuren op het moment t0? (het evenwicht wordt op dat moment bereikt)
- Op het moment tp wordt het evenwicht verstoord door toevoeging van twee stoffen. Welke stoffen?
Na enige tijd wordt een nieuw evenwicht bereikt.
- Wat is de winst nu wat betreft productvermeerdering?
Je hebt een systeem in chemisch evenwicht en je gaat dat systeem afkoelen (je onttrekt warmte-energie). Normaal en volgens de regels van Le Chatellier en van 'tHoff zal dan het evewicht een verschuiving ondergaan:
De exotherme reactie (die energie produceert) zal extra gaan verlopen.
Maar daar is niet alles mee gezegd: Zich aanpassen aan een verandering kost namelijk tijd. Afkoeling zal voor de deelnemende deeltjes in het evenwicht betekenen dat ze langzaamaan trager gaan bewegen en hun vibratie neemt ook af.
Maar stel nu eens dat je het evenwicht plotseling heel snel afkoelt: in een paar seconden valt de temperatuur vele graden omlaag (de stoffen worden bijvoorbeeld in ijs gegooid, of erger: in vloeibare stikstof).
Dan heeft het systeem geen tijd om zich rustig aan te passen. Alle deeltjes vallen vrijwel meteen stil, verliezen hun beweging.
Deeltjes zonder voldoende energie doen niet mee aan een reactie. Elke reactie heeft dan ook een minimumtemperatuur. Daaronder verloopt de reactie niet.
Als een evenwichtsreactie supersnel heel erg wordt afgekoeld, dan zeggen we ook wel:
het evenwicht wordt bevroren.
De heen- en terugreactie komen allebei in één klap stil te liggen en hebben geen tijd om zich aan de verandering aan te passen. Zowel de producten als de uitgangsstoffen komen in één klap onder hun minimum temperatuur.
Zonder reacties zullen dus vervolgens ook geen concentraties veranderen. Er is geen sprake meer van een dynamisch evenwicht; de dynamiek is er uit.
Opdracht 10
Leg uit in je eigen woorden waarom bevriezing van een evenwicht meteen het einde betekent van de dynamische toestand.
Opdracht 11
Bacteriën veranderen vrijwel niet als je ze snel invriest.
Alle stoffen blijven met gelijke concentraties aanwezig en het metabolisme blijft werkloos gesloten bij die koude.
Ga je voorzichtig weer opwarmen dan zullen vele reacties in die bacteriën langzaamaan hun activiteit weer hernemen. De bacteriën komen weer tot leven.
Er zijn mensen die dit verschijnsel op zichzelf willen toepassen: je laat je invriezen vlak voor je dood gaat. Wie weet kun je weer lekker warm worden als je over honderd jaar (als er nieuwe geneesmiddelen zijn uitgevonden) weer voorzichtig wordt opgewarmd.
Wat vind je van dit idee? Technisch zowel ethisch?
Opdracht 12
Bewering: Een enzym dat de evenwichtsreacties beïnvloedt kan de waarde van K veranderen.
Is die bewering waar of vals? Leg uit.
antwoord 08-12
Je weet dat een katalysator de chemische reactiesnelheid kan beïnvloeden.
Let op: het kan een positieve katalysator zijn (die versnelt de reactie), maar ook een negatieve (die vertraagt de reactie)
In geval van een chemisch evenwicht worden de twee reacties in gelijke mate beïnvloed. De heen-reactie wordt even sterk beïnvloed als de terugreactie.
Opdracht 13
Stel je voor dat je de twee reacties van een evenwicht precies op dezelfde manier beïnvloedt; leg uit of het evenwicht dan verplaatsing ondergaat en of het evenwicht dynamisch blijft.
Wat is dan de noodzaak om een katalysator toe te passen als die toch niets verandert aan de ligging van het evenwicht?
Het antwoord op die vraag heeft te maken met de tijd die nodig is om het evenwicht te bereiken. Zolang het evenwicht nog moet worden ingesteld (en dat kan soms heel lang duren en heel moeizaam gaan) kan zo'n katalysator zeker zinvol zijn.
De reacties kunnen traag zijn. Een katalysator kan zo de periode tot te verkorten, van uren, dagen, jaren tot misschien maar minuten of seconden.
Sommige evenwichten worden in de praktijk nooit en te nimmer bereikt zonder katalysator.
Bij levende wezens noemt men de katalysatoren: bio-katalysatoren of ook: enzymen.
Het is nu eenmaal zo dat de meeste reacties van het metabolisme (stofwisseling) evenwichtsreacties zijn. Het zal dus duidelijk zijn dat enzymen hier ook altijd dienen om die evenwichten in het metabolisme binnen de juiste tijd te bereiken, te realiseren.
Het menselijk lichaam heeft duizenden verschillende enzymen, allemaal zeer specifiek. Zonder die enzymen geen metabolisme.
Opdracht 14
Schets een diagram dat de eventuele invloed laat zien van een katalysator op de reactiesnelheden binnen een evenwicht.
Voor de liefhebbers kan het leuk zijn om het principe van Van 't Hoff nog eens wiskundig na te kijken bij Wikipedia
Stel dat alle stoffen die meedoen aan een evenwicht homogene stoffen zijn, dan noemen we ook het evenwicht een homogeen evenwicht. Elke stof die meedoet heeft een of andere concentratie (in geval van oplossingen en vloeistoffen) of druk (in geval van gassen).
Het volgende evenwicht is heterogeen: CaCO3(s)  CO2(g) + CaO(s)
CO2(g) + CaO(s)
Stel je een gesloten reactievat voor met een bepaalde hoeveelheid calciumcarbonaat op de bodem. Dat wordt flink verhit totdat het calciumcarbonaat gaat ontleden. Daarbij vormen zich het gas kooldioxide en ongebluste kalk (CaO).
In het reactievat (onder de zuiger) heerst een chemisch evenwicht tussen de twee vaste stoffen (heterogeen op de bodem) en het gas (homogeen verspreid door de ruimte in het vat). De enige stof met een concentratie dan wel druk is hier het gas kooldioxide.
Vaste stoffen krijgen in de vergelijking, in de formule voor de evenwichtsconstante de waarde 1. Dat is zo afgesproken voor heterogene stoffen.
Opdracht 15
Leg de volgende wiskundige uitdrukking uit met de bovenstaande informatie:
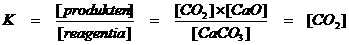
Een ander voorbeeld van een heterogeen evenwicht is de dissociatie van een onoplosbaar zout in water.
Het woord "onoplosbaar" is niet exact, want er zullen toch altijd wat ionen aan het rooster ontsnappen als het zout in water is. De ontsnapte ionen (de producten) reageren graag terug om het zout te vormen.
Het volgende evenwicht stelt zich in:
CaCO3(s)  Ca2+(aq) + CO32-(aq)
Ca2+(aq) + CO32-(aq)
Van de vier componenten in dit mengsel is één het oplosmiddel en drie doen mee aan de eigenlijke reactie.
Opdracht 16
Van de drie componenten die deelnemen aan de chemische reactie, welke zijn heterogeen en welke homogeen?
Alleen de ionen hebben een concentratie die ingevuld kan worden in de evenwichtsconstante:
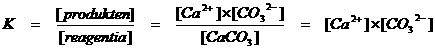
K is dus de evenwichtsconstante. Het is een quotiënt met boven de streep de concentraties van de producten en onder de streep de concentraties van de reagentia. Als die concentraties gelijk zijn, dan heeft K de waarde 1.
K=1 betekent dus dat er sprake is van een mooi evenwichtig evenwicht; gelijk aan beide kanten.
Heel veel evenwichten echter zijn helemaal niet zo mooi gelijk aan beide kanten. We zagen hiervoor al het voorbeeld van een slecht oplosbaar zout in water. Als er aan één kant van het evenwicht heel veel deeltjes zijn en aan de andere kant veel en veel minder, dan ligt het evenwicht eenzijdig, aan één kant. Dat is altijd de kant van de zwakkere stoffen, de stoffen die het moeilijkst reageren.
De waarde van K is dan heel groot of juist heel klein. Aan de waarde van K kun je dus meteen zal zien hoe de ligging van het evenwicht is.
De evenwichtsconstante bevat alleen de concentraties van de stoffen die homogeen aanwezig zijn. In dit geval voeg je een C toe aan de K: KC .
Een andere homogene situatie is het geval van een gas-evenwicht. Dan spreken we niet zozeer van concentraties, maar wel van de (partiële) gasdruk van elk deelnemend gas. Elk gas in een gasmengsel draagt bij aan de druk.
De partiële druk van elke component is evenredig met de hoeveelheid van dat gas.
In de formule van de evenwichtsconstante vullen we hier de waarden in van die partiële drukken; de formule verandert niet in werkelijkheid, maar de K wordt soms aangegeven met KP.
resumerend:
- In homogene oplossingen gebruiken we KC
- Bij gassen gebruiken we KP
- Bij heterogene mengsels (s)+(aq) in evenwicht gebruiken we Ks (zie volgende paragraaf)
- Volgens afspraak wordt de "concentratie" van een vaste, heterogene stof de waarde 1 gegeven.
- De waarde van K hangt niet af van veranderingen in concentraties, druk of van de aanwezigheid van een katalysator,
Die waarde verandert alleen als de temperatuur van het systeem in evenwicht verandert.
Er zijn veel evenwichten met extreem sterke stoffen aan één kant en heel zwakke stoffen aan de andere kant van de pijlen.
Nogmaals: als evenwicht bereikt is kunnen de concentraties aan beide kanten zeer verschillend zijn. Vrijwel zeker zal er heel veel zijn van de zwakke en heel weinig van de sterke stoffen.
Zo'n evenwicht ligt sterk aan één kant.
Dat zie je meteen aan de formule voor K en de waarde van K:
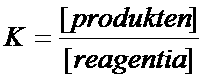
Opdracht 17
Welke waarde heeft K:
- als er zeer sterke producten en zeer zwakke reagentia meedoen
- als er zeer zwakke producten en zeer sterke reagentia meedoen
antwoord 08-17
Zouten kunnen goed of slecht oplossen in water, dus veel of weinig ionen produceren, vrijgeven aan het water. De ionen van het opgeloste zout bereiken dan een zekere concentratie en het wiskundige product van deze ionconcentraties noemen we: het Ionenproduct.
Opdracht 18
Als je 29 gram NaCl oplost in één liter water, wat is dan de concentratie?
[Na+] = ......... mol/l e [Cl-] = ........ mol/l. Oftewel, het ionenproduct = ............. mol2/l2
Er is altijd wel een ionenproduct, maar niet altijd een oplosbaarheidsproduct. Dat is er alleen voor zouten die niet goed oplossen.
Een "evenwicht" komt pas in zicht als het gaat over slecht oplosbare zouten.
Bijvoorbeeld:
Zilverchloride is een onoplosbaar zout (beter: slecht oplosbaar zout). Echt onoplosbaar zijn zouten vrijwel nooit. Altijd lost er wel een klein beetje op in water. Altijd blijft wel de mogelijkheid voor de ionen in het rooster om daaruit te ontsnappen en het water in te trekken.
Als ze niet allemaal kunnen vrijkomen, omdat het rooster te sterk is bijvoorbeeld, dan krijg je op den duur een evenwichtssituatie waarin de vrije ionen in dynamisch evenwicht zijn met de onvrije in het rooster. Ze ontsnappen, maar zodra positieve en negatieve ionen elkaar tegenkomen, vormen ze weer een rooster.
AgCl(s)  Ag+(aq)+ Cl-(aq)
Ag+(aq)+ Cl-(aq)
Opdracht 19
Bij het merendeel van dit type evenwichten is de heenreactie endotherm.
Wat gebeurt er dus met het ionenproduct bij het verwarmen van het mengsel?
Na het bereiken van het evenwicht en als we de temperatuur constant houden, zullen de concentraties niet meer veranderen.
(let op: de vaste stof AgCl is heterogeen en heeft dus geen concentratie.
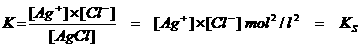
Zo zal elk zout met een kleine oplosbaarheid een KS hebben, genoemd: Oplosbaarheidsproduct
Je kunt dus een slecht oplosbaar zout een heel klein beetje oplossen. Eerst is er een stijgend ionenproduct, maar al heel gauw is het maximum daarvan bereikt: dan is het ionenproduct gelijk aan het oplosbaarheidsproduct. De oplossing is "verzadigd": bij deze bepaalde temperatuur kan niet méér oplossen.
Elk tabellenboek heeft een tabel met de oplosbaarheidsproducten van zouten.
We hebben hier een tabel die ongeveer aangeeft of een zout oplosbaar is.
Het zout zal een evenwicht bereiken met zijn ionen, dus dan veranderen de concentraties niet meer.
Het ionenproduct heeft zijn maximale waarde bereikt = het oplosbaarheidsproduct.
Opdracht 20
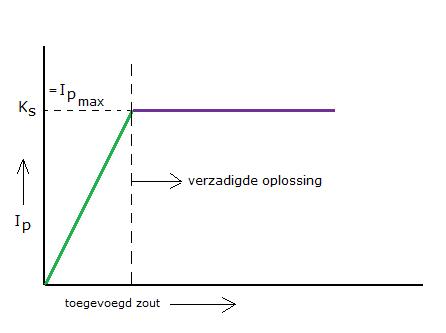
Leg het verloop van het diagram uit.
N.B. kijk uit om het oplosbaarheidsproduct en de eigenlijke oplosbaarheid van een zout niet te verwarren met elkaar!
De oplosbaarheid is het aantal MOL van het zout dat per liter water oplossen kan.
De KS is het product van de ionenconcentraties van het zout in een verzadigde oplossing.
Zowel de oplosbaarheid S als heet oplosbaarheidsproduct Ks zijn mede afhankelijk van de temperatuur.
Uitvoerige uitleg over het oplosbaarheidsproduct en over oplosbaarheid vind je op wikipedia.
In wateroplossingen zijn altijd watermoleculen in ongelooflijke hoeveelheden, die voortdurend met elkaar in contact zijn.
Elk watermolecuul heeft de (zwakke) neiging om protonen af te staan en op te nemen; tijdens zo'n ontmoeting kan dan het volgende gebeuren:
| H2O |
+ |
H2O |
 |
H3O+ |
+ |
OH- |
|
ΔH |
> 0 |
| zwakke base |
|
zwak zuur |
|
sterk zuur |
|
sterke base |
|
|
|
Let er op dat de beide ionen H3O+ en OH- in gelijke hoeveelheden worden gevormd. Het waterevenwicht kan alleen bestaan in waterig milieu en ligt heel ver naar één kant (de kant van ongesplits water), dus met weinig producten. De evenwichtsconstante zal dus klein zijn.
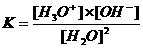

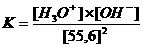

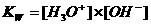
Opdracht 21
Wat is de wiskundige relatie tussen K en Kw?
In neutrale waterige oplossingen bij 25ºC, gebeurt het volgende:
Van elke MOL watermoleculen (dat zijn er 6 x 1023) zullen er "slechts" 6 x 1016 een proton vangen en tegelijkertijd zullen eenzelfde hoeveelheid andere watermoleculen een proton afstaan.
Opdracht 22
Hoeveel watermoleculen doen actief mee met de protonenoverdracht in 18 gram water (=18 ml)?
Hoeveel watermoleculen zijn dat?
Dus, in water van 25ºC:
[H3O+] = [OH-] = 10-7 mol/dm3
ofwel:
pH = pOH = 7
Kw (de evenwichtsconstante van de autoprotolyse) = K x (55.6)2 = [H3O+] x [OH-] = 10-14 mol2/l2
Opdracht 23
De autoprotolyse van water is een endotherm proces. Wat gebeurt er met het evenwicht als water wordt verwarmd?
Opdracht 24
Bewering:
"Zuiver en neutraal kokend water (met een temperatuur van 100oC) heeft geen pH=7"
Leg uit of en waarom deze bewering waar of onwaar is.
antwoord 08-24

 2HI
2HI
 I2+ H2
of:
I2 + H2
I2+ H2
of:
I2 + H2  2HI
2HI
 2HI (ΔH < 0)
2HI (ΔH < 0)
 I2+ H 2 (ΔH > 0)
I2+ H 2 (ΔH > 0)
 2NH3 (ΔH < 0 en ΔS < 0)
2NH3 (ΔH < 0 en ΔS < 0)
 I2 + H2
I2 + H2


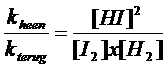
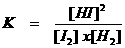
 saccharose + water ΔH < 0
saccharose + water ΔH < 0

 H++ In-
H++ In-
 de gele kleur domineert.
de gele kleur domineert.

 H++ In-
H++ In-

 H++In-
H++In-

 saccharose + water ΔH < 0]
saccharose + water ΔH < 0]
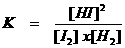
 2Ag(s)+ C6H12O7 + 2H+ ΔH > 0 ( evenw. 1)
2Ag(s)+ C6H12O7 + 2H+ ΔH > 0 ( evenw. 1)
 Ag(NH3)2+
Ag(NH3)2+
 HbO2 + H+
HbO2 + H+
 H2CO3
H2CO3
 H+ + HCO3-
H+ + HCO3-
 NH3(aq)
NH3(aq)
 NH4+ + OH-
NH4+ + OH-

 CO2(g) + CaO(s)
CO2(g) + CaO(s)
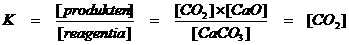
 Ca2+(aq) + CO32-(aq)
Ca2+(aq) + CO32-(aq)
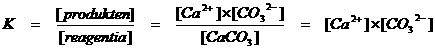
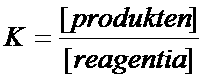
 Ag+(aq)+ Cl-(aq)
Ag+(aq)+ Cl-(aq)